Geometry PA
The purpose of this lab is for you to:
- Practice basic C programming:
- Using structs and non-trivial loops (i.e. something more interesting than
for (int i = 0; i < n; i++)) - Writing functions
- Using several different libraries (i.e.
.h/.cfiles) in a single program.
- Using structs and non-trivial loops (i.e. something more interesting than
- Learn how to read an algorithm specification and write working code from it.
- Practice working at the appropriate level of abstraction.
- Solve problems in computational geometry, an important and fascinating domain of computer science and mathematics.
Getting Started
First download and decompress one of the starter files:
Don't forget to download the appropriate Makefile for your platform from Piazza or the course website.
Starter Code
The starter code has 8 files. Four of these are modules that we are providing you, and you should not need to edit these:
geometry.handgeometry.c: A library of relatively simple functions for manipulating geometrical objects (called primitives).turtle.handturtle.c: The turtle graphics library.
The files you need to edit are:
main.c: Your main program.pa1.handpa1.c: A small library of geometry tools that you are going to write.testsuite.c: The public tests for this assignment. You may want to try adding your own tests.
Be sure to add the following to your Makefile:
MODS=geometry.o turtle.o pa1.o
LIBS=-lm
This tells your Makefile to build the geometry, turtle, and pa1 modules and include the math library (libm.so) when linking.
Computational Geometry: A (Very, very, basic) Introduction
Computational geometry is a sub-field of computer science that focuses on algorithms and data-structures for solving geometric problems. A few typical examples of computational geometry in action are:
- robot navigation (obstacles are polygons in the robots workspace),
- map overlays (finding areas of special interest on a map),
- computer aided design (CAD systems allow designers to build "working" models of products in 3D),
- protein folding (researchers are trying to understand how proteins fold in order to combat diseases like mad-cow disease and are using computational geometry to do it--ask Dr. Bowers about this if you are interested),
- and a lot more.
It is also related to several other areas of computer science including (but not limited to): computer vision, graphics, bioinformatics.
Polygons
In this PA you are going to be writing a few basic algorithms and data structures for dealing with polygons and for computing something called the "convex hull" of a polygon.
For our purposes a polygon is a drawing in the plane (i.e. on a flat sheet of paper) created by first putting the pen down at some start location, then drawing a series of straight line segments without lifting pen until eventually ending up back at the start location.
The points at which one line segment ends and the next begins are called the vertices and the line segments themselves are called the sides of the polygon. (These are also often called edges.)
You are already familiar with lots of different polygons. For instance, triangles, squares, rectangles, pentagons, octagons, dodecagons (you all know what a dodecagon is, right?). All of these things are formed by a bunch of straight line segments (the sides) connected end-to-end (at the vertices). All of these have something else in common--they are all simple, meaning that they do not self intersect. We will restrict our discussion to simple polygons.

Geometry Primitives Library
Included in the starter code for this PA is a small geometry primitives library. The word primitives is used to denote basic data structures and algorithms that are used to build more complex data structures and algorithms. This is much the same as the difference between primitive types, like int and char and the compound types you create using structs in C or classes in Java.
The geometry library includes the following two structures (see geometry.h):
/*
* 2D points (x,y)
*/
typedef
struct {
int x;
int y;
} point_t;
/*
* 2D line segments ((x1, y1), (x2, y2));
*/
typedef
struct {
point_t p1;
point_t p2;
} segment_t;
The first, point_t is used to specify 2D points (i.e. (x, y)) in the plane with integer coordinates. The second, segment_tspecifies a line segment between its two points (p1, p2). These structures may be useful for you in the remainder of this PA and you can use them in your code.
The geometry library also defines several predicate functions, which are functions that return true or false based on some property. We will discuss these functions later as they become relevant.
Problem 1: Drawing a triangle
Write a function called drawTriangle which takes as input three point_ts, p_1, p_2, and p_3 and draws the triangle. In other words, your function's signature should be:
void draw_triangle(point_t p1, point_t p2, point_t p3);
Note that you should declare your function in pa1.h and define it in pa1.c.
Use your function to draw several different triangles in the main() function in main.c.
Reference solution: ~5-10 lines
Problem 2: Struct for storing polygons
We store a polygon as a list of vertices. The edges are inferred by connecting adjacent vertices in the list by line segments. In geometry.h we have defined a type polygon_t for storing a polygon. It looks like this:
typedef
struct {
point_t* vertices;
int num_vertices;
} polygon_t;
Note that this stores the vertices as a dynamically-allocated array called vertices.
Write a function that can create a polygon_t from an array of vertices.
Add the following function declaration to pa1.h:
polygon_t create_polygon(point_t vertices[],
int num_vertices);
Define the create_polygon function in pa1.c. It should create and return a new polygon_t struct with the points from the input attribute vertices copied into the vertices attribute of the struct. Note that this will require first allocating enough memory to store vertices.
You should also implement the following function:
void free_polygon(polygon_t *poly);
This function should free any allocated memory associated with the given polygon (setting pointers to NULL as appropriate) and should should also set the number of vertices in that polygon to zero. This function should be called by client programs for each polygon used in order to prevent memory leaks.
Note that this function is passed a polygon pointer; this will allow you to reset any de-allocated pointers and prevent dangling pointer problems.
Reference solution: ~15-20 lines
Problem 3: Drawing a polygon
Write a function called draw_polygon which takes as input a polygon_t (as you defined above) and draws the polygon. In other words, your function's signature should be:
void draw_polygon(polygon_t poly);
Declare your function in pa1.h and define it in pa1.c.
Use your function to draw several different polygons in the main() function in main.c (with different numbers of points in each polygon).
Reference solution: ~10-15 lines
Convex Polygons
One classification of polygons that is important for many computational purposes is the difference between convex and non-convex polygons.
A convex polygon is one where all the interior angles are less than 180 degrees. If even one angle is greater than 180 degrees, then the polygon is non-convex. See below:

Suppose you wanted to check if a polygon were convex or not. You could compute all of the angles at each vertex and test whether any one is greater than 180 degrees. The problem with this approach is that it requires you to use transcendental functions like sin() and cos() to compute the angles. When possible, we often avoid the use of these functions. One reason to avoid the use of these trig functions is that they require many more processor cycles to compute than simple arithmatical operations like addition and multiplication.
Another method for determining whether a polygon is convex is to walk around the polygon (think of redrawing it with the pen, or better yet, drawing it in the grass and walking along it) and keep track of how many left-hand-turns you make and how many right-hand-turns you make. (Whether a turn is a left-hand-turn or right-hand-turn can be computed with only simple arithmetic and without computing the angle or using trig functions.)
Notice that if the polygon is convex, then either 1) all of your turns will be right-hand-turns (if you are walking clockwise), or 3) they will all be left-hand-turns (if you are walking counter-clockwise). However, on a non-convex polygon, you always have a mix of right and left-hand-turns. In the geometry library there are two functions you will need:
-
is_left_hand_turn(point_t p1, point_t p2, point_t p3): Returns true if and only if traveling from p1 to p2 and then from p2 to p3 consitutes a left-hand-turn. -
is_right_hand_turn(point_t p1, point_t p2, point_t p3): Returns true if and only if traveling from p1 to p2 and then from p2 to p3 constitutes a right-hand-turn.
Problem 4: Convex test for 4-gons
A 4-gon is a polygon with 4 sides (for example, squares, parallelograms, rectangles, kites, diamonds, etc.). Write a function called is_4gon_convex with the following signature:
bool is_4gon_convex(point_t p1, point_t p2, point_t p3, point_t p4);
The input to this function is the four vertices of the 4-gon, (p1, p2, p3, p4) and output is true if and only if the 4-gon is convex, false otherwise.
You may wish to write a function called draw_4gon which takes as input the four points p1, p2, p3, p4 of a 4-gon and draws it blue if it is convex, or red otherwise. (Hint: use your is_4gon_convex function). Draw at least one convex and one non-convex 4-gon in your main() function in main.c.
Optional Challenge Question: Remember that we are assuming the input polygon is simple, i.e. it doesn't self-cross. Does your method always work correctly when the polygon is not simple?
Reference solution: ~10-15 lines
Problem 5: Convex test for polygons
Write a function called is_polygon_convex with the following signature:
bool is_polygon_convex(polygon_t poly);
The input to this function is a polygon (of type polygon_t which you defined above) and the output is true if and only if the polygon poly is convex, false otherwise.
Modify your draw_polygon function to draw the polygon blue if it is convex, red otherwise.
Hint 1: if you get stuck, think about writing a test for 5-gons, and then 6-gons. What is changing each time?
Hint 2: You might want to count the number of left hand turns and count the number of right hand turns you find. If both are non-zero, then you have a mix.
Hint 3: Remember that it takes 3 consecutive vertices to check whether something is a turn. Did you check all of the vertices (where does your loop end)?
Reference solution: ~15-20 lines
Convex Hulls
One very important concept from computational geometry is the convex hull of a polygon. The convex hull of a polygon P is the smallest convex polygon that contains P on its interior. See the figure below. Convex polygons are generally easier to work with computationally than non-convex polygons. Because of this, there are many applications that use the convex hulls to speed up computation.
For instance, in computer graphics applications such as a game or simulation you might have polygonal objects moving around and want to test whether two objects collide with one another. It turns out that testing whether two non-convex polygons have collided is a much more expensive operation than testing whether two convex polygons have collided.
A system for testing collisions for a bunch of non-convex polygons could simply test directly whether each polygon collides with every other polygon (slow), or instead it could store the convex hull of each polygon and as a first test determine whether any of the convex hulls collide (fast). The system would then only test whether the actual polygons collide if their convex hulls collide. Thus the slow operation is invoked only when it is more likely to return true.
An example of a convex hull is shown below:
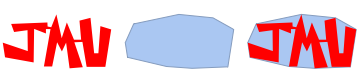
The left of the image above shows a very non-convex polygon in red spelling out the letters JMU. The convex hull of the JMU-polygon is shown in the middle, and on the right the JMU polygon is shown on top of its convex polygon. You can think of the convex hull as what you get if you stretch a rubber-band around the polygon.
Problem 6: Drawing convex hulls
For this exercise you are going to draw the convex hull of a polygon. The essential idea for this is to take all pairs of vertices (not necessarily consecutive) and test the pair to see if all other points in the polygon are either ALL left-hand-turns or ALL right-hand-turns from that pair. The basic pseudo-code for this function is:
For all pairs (p, q):
If all other points form a left-hand-turn with (p, q) or all other
points form a right-hand-turn with (p, q):
Draw the line segment (p, q)
Otherwise:
Do not draw (p, q)
Your function should have the following signature:
void draw_convex_hull(polygon_t poly);
Note: When testing your code, you should only use polygons for which no three points are collinear. The pseudo-code above assumes that the polygon is "generic" which means no three points are collinear.
Reference solution: ~25-40 lines
Submission
DUE DATE: Friday, September 25, 2015 at 23:59 EDT (11:59pm)
Submit ONLY your completed pa1.h and pa1.c file on Canvas using the appropriate assignment submission. Submit both files separately; do NOT submit a zip file. Make sure both files contain a comment field at the top with your name and a statement of compliance with the JMU honor code.
Please check your code carefully and make sure that it complies with the project specification. In addition, make sure that your code adheres to general good coding style guidelines. Fix any spelling mistakes, incorrect code formatting, and inconsistent whitespace before submitting. Make sure you include any appropriate documentation.
